The Many Faces of Spin

Many of nature's deepest mysteries come in threes. Why does space have three spatial dimensions (ones that we can see, anyway)? Why are there three fundamental dimensions in physics (mass M, length L and time T)? Why three fundamental constants in nature (Newton's gravitational constant G, the speed of light c and Planck's constant h)? Why three generations of fundamental particles in the standard model (e.g. the up/down, charm/strange and top/bottom quarks)? Why do black holes have only three properties—mass, charge and spin? Nobody knows the answers to these questions, nor how or whether they may be connected. But some have sought for clues in the last-named of these properties: spin.

Spacetime is warped and twisted by the
mass and spin of the earth.

We are all familiar with rotation in the macroscopic world of tops, ballet dancers, planets and galaxies. Spin in the microscopic world is subtler, and obeys rules that are at once familiar (e.g. conservation of angular momentum) and bizarrely counter-intuitive (e.g. quantization and half-integer spin for fermions, which in the macroscopic world would correspond to objects that rotate through 720 rather than 360 degrees before returning to their original states). More abstract still are quantities like "isospin", which is analogous to ordinary spin in some ways but governs the behavior of the strong and weak nuclear forces (rotation through 180 degrees of isospin, for instance, converts a proton into a neutron), and torsion, a mathematical term related to the intrinsic twist of spacetime (this appears in some extensions of general relativity, but Einstein himself set it to zero in general relativity for reasons of logical economy). Are there connections between these manifestations of spin in the worlds of the large and small? Do they hint at the direction in which Einstein's theory of gravity might need to be extended in order to unify it with the other forces of nature? A generation of physicists since Einstein have thought about these questions, and they are part of the reason what makes Gravity Probe B so important, not just as another test of general relativity, but as a source of new insights about spacetime itself. Nobel laureate C.N. Yang wrote in a letter to NASA Administrator James M. Beggs in 1983 that general relativity, "though profoundly beautiful, is likely to be amended ... whatever [the] new geometrical symmetry will be, it is likely to entangle with spin and rotation, which are related to a deep geometrical concept called torsion ... The proposed Stanford experiment [Gravity Probe B] is especially interesting since it focuses on the spin. I would not be surprised at all if it gives a result in disagreement with Einstein's theory."

Back to Top

Gravito-Electromagnetism

In general situations, space and time are so inextricably bound together in general relativity that they are hard to separate. In special cases, however, it becomes feasible to perform a "3+1 split" and decompose the metric of four-dimensional spacetime into a scalar time-time component, a vector time-space component and a tensor "space-space" component. When gravitational fields are weak and velocities are low compared to c, then this decomposition takes on a particularly compelling physical interpretation: if we call the scalar component a "gravito-electric potential" and the vector one a "gravito-magnetic potential", then these quantities are found to obey almost exactly the same laws as their counterparts in ordinary electromagnetism! (Although little-known nowadays, the idea of parallels between gravity and electromagnetism is not a new one, and goes back to Michael Faraday's experiments with "gravitational induction" beginning in 1849.) One can construct a "gravito-electric field" g and a "gravito-magnetic field H from the divergence and curl of the scalar and vector potentials, and these fields turn out to obey equations that are identical to Maxwell's equations and the Lorentz force law of ordinary electrodynamics (modulo a sign here and a factor of two there; these can be chalked up to the fact that gravity is associated with a spin-2 field rather than the spin-1 field of electromagnetism). The "field equations" of gravito-electromagnetism turn out to be of great value in interpreting the predictions of the full theory of general relativity for spinning test bodies in the field of a massive spinning body such as the earth — just as Maxwell's equations govern the behavior of electric dipoles in an external magnetic field. From symmetry considerations we can infer that the earth's gravito-electric field must be radial, and its gravito-magnetic one dipolar, as shown in the diagrams below:

These facts allow one to derive the main predictions of general relativity that are of relevance to Gravity Probe B, simply by replacing the electric and magnetic fields of ordinary electrodynamics by g and H respectively (for an illuminating discussion see Kip Thorne's contribution to Near Zero: New Frontiers of Physics, 1988). Based on this analogy the term "gravito-magnetic effect" is sometimes used interchangeably with "frame-dragging" (or with "Lense-Thirring effect"; see below). However any such identification must be treated with care because the distinction between gravito-magnetism and gravito-electricity is frame-dependent, just like its counterpart in Maxwell's theory. This means that observers using different coordinate systems (as, for example, one centered on the earth and another on the barycenter of the solar system) may disagree on the relative size of the effects they are discussing. Gravito-electromagnetism has already been indirectly observed in the solar system for some time, since general relativistic corrections are routinely used in, for instance, updating the ephemeris of planetary positions, and gravito-electromagnetic fields are nothing more than a necessary limit of Einstein's gravitational field in situations where gravity is weak and velocities are low. This is different from measuring a gravito-electromagnetic phenomenon like frame-dragging directly, which is one of the two primary goals of the Gravity Probe B mission.

Back to Top

Geodetic Effect

The geodetic effect provides us with a sixth test of general relativity (after the three classical tests plus Shapiro delay and the binary pulsar), and it is the first one to involve the spin of the test body. The effect arises in the way that angular momentum is transported through a gravitational field in Einstein's theory. Einstein's friend and colleague Willem de Sitter (1872-1934), who was instrumental in making general relativity known abroad, began to study this problem when the theory was less than a year old. He found that the earth-moon system would undergo a precession in the field of the sun, a special case now referred to as the de Sitter or "solar geodetic" effect (although "heliodetic" might be more descriptive). De Sitter's calculation was extended to rotating bodies such as the earth by two of his countrymen: in 1918 by the mathematician Jan Schouten (1883-1971) and in 1920 by the physicist and musician Adriaan Fokker (1887-1972).

De Sitter	Schouten	Fokker

In the framework of the gravito-electromagnetic analogy, the geodetic effect arises partly as a spin-orbit interaction between the spin of the test body (the gyroscope in the case of GP-B) and the "mass current" of the central body (the earth). This is the exact analog of Thomas precession in electromagnetism, where the electron experiences an induced magnetic field (in its rest frame) due to the apparent motion of the nucleus. In the gravitomagnetic case, the orbiting gyroscope feels the massive earth whizzing around it (in its rest frame) and experiences an induced gravitomagnetic torque, causing its spin vector to precess. This spin-orbit interaction accounts for one third of the total geodetic precession; the other two thirds arise due to space curvature alone and cannot be interpreted gravito-electromagnetically. They can, however, be understood geometrically. Model flat space as a 2-dimensional sheet, as shown in the diagram below (left).

Geodetic precession and the "missing inch"

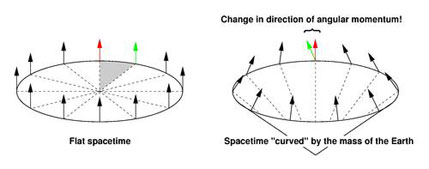
A gyroscope's spin vector (arrow) points at right angles to the plane of its motion, and its direction remains constant as the gyroscope completes a circular orbit. If, however, we fold space into a cone to simulate the effect of the presence of the massive earth (right), then we must remove part of the area of the circle (shaded) and the gyroscope's spin vector no longer lines up with itself after making a complete circuit (green and red arrows). The difference between these two directions (per orbit) makes up the other two thirds of the geodetic effect. In the case of Gravity Probe B this is sometimes referred to as the "missing inch" argument because space curvature shortens the circumference of the spacecraft's orbital path around the earth by 1.1 inches. In polar orbit at an altitude of 642 km the total geodetic effect (comprising both the spin-orbit and space curvature effects) causes a precession in the north-south direction of 6606 milliarcsec/yr — an angle so small that it is comparable to the average angular size of the planet Mercury as seen from earth.

Geodetic Effect

Experimental detection (or non-detection) of the geodetic effect will place new and independent limits on alternative theories of gravity known as "metric theories" (loosely speaking, theories that respect Einstein's equivalence principle). These theories are characterized by the Eddington or Parametrized Post-Newtonian (PPN) parameters β and γ, which are both equal to one in general relativity. The geodetic effect is proportional to (1+2γ)/3, so a confirmation of the Einstein prediction at the level of 0.01% would translate into comparable constraint on γ — more stringent than all but the most recent Shapiro time-delay test based on data from Cassini. Gravity Probe B observations of geodetic precession could also impose new constraints on other "generalizations of general relativity" such as the scalar-tensor theories pioneered by Carl Brans and Robert Dicke in 1961 (see Kamal Nandi et al, 2001). Another such class of theories incorporates torsion into Einstein's theory; examples have been proposed by Kenji Hayashi and Takeshi Shirafuji (1979), Leopold Halpern (1984) and Yi Mao et al. (2006). Another is based on extending the theory to higher dimensions; constraints on such theories arising from the geodetic effect have been discussed by Dimitri Kalligas et al. (1995) and Hongya Liu and James Overduin (2000). The most recent kind of generalization involves violations of Lorentz invariance, the conceptual foundation of special relativity; implications of such theories for Gravity Probe B have been worked out by Quentin Bailey and Alan Kostelecky (2006).

Back to Top

Frame-Dragging Effect

Lense

Thirring

The frame-dragging effect, the seventh test of general relativity and the second one to involve the spin of the test body, reveals most clearly the Machian aspect of Einstein's theory. In fact, it is curious that Einstein did not work out this effect himself, given that he had obtained explicit frame-dragging effects in all his previous attempts at gravitational field theories, and that he still regarded Mach's principle as the philosophical pillar of general relativity in 1918. Whatever the reason, it was not until that year that the general-relativistic frame-dragging formula was derived by Hans Thirring (1888-1976) and Josef Lense (1890-1985), after whom the effect is now usually named. In an ironic twist, Thirring had not intended to do calculations at all; he had wanted to build a frame-dragging experiment (a cylindrical version of Föppl's flywheel experiment) and only settled for theoretical work after he was unable to arrange the necessary financing (see Herbert Pfister's contribution to Mach's Principle: From Newton's Bucket to Quantum Gravity, 1995). Thirring's initial result described the gravitational field inside a rotating cylinder; his second calculation (with Lense) involved the field outside a slowly rotating solid sphere and forms the basis for experimental tests such as Gravity Probe B. Both results are "Machian" in the sense that the inertial reference frame of a test particle is strongly influenced by the properties of the larger mass (the cylinder or sphere). This is completely unlike Newtonian dynamics, where a test particle's inertia is defined only by its motion with respect to "absolute space" and is unaffected by the distribution of matter. In fact, with the right parameters it is possible for a large mass in general relativity to completely "screen" the background geometry, so that a test particle feels only the reference frame defined by that mass. This phenomenon is known as "total" or "perfect dragging" of inertial frames (more on this below).

Frame-dragging Effect

Frame-dragging in realistic experimental situations is not nearly that strong and the utmost ingenuity has to be exercised to detect it at all. Analyzed in terms of the gravito-electromagnetic analogy, the effect arises due to the spin-spin interaction between the gyroscope and rotating central mass, and is perfectly analogous to the interaction of a magnetic dipole μ with a magnetic field B (the basis of nuclear Magnetic Resonance Imaging or MRI). Just as a torque μ×B acts in the magnetic case, so a gyroscope with spin s experiences a torque proportional to s×H in the gravitational case. For Gravity Probe B, in polar orbit 642 km above the earth, this torque causes the gyroscope spin axes to precess in the east-west direction by a mere 39 milliarcsec/yr — an angle so tiny that it is equivalent to the average angular width of the dwarf planet Pluto as seen from earth.

Back to Top

Genesis of GP-B

How small is 1/10th of a milliarcsecond?

As the calculations of de Sitter, Schouten and Fokker became more widely known, particularly through Arthur Eddington's influential textbook The Mathematical Theory of Relativity (1923), experimentalists began to take interest. P.M.S. Blackett (1897-1974) considered looking for the de Sitter effect with a laboratory gyroscope in the 1930s, but concluded (rightly) that the task was hopeless with existing technology. To see what makes the problem so challenging, consider the gyroscope rotor shown below. The de Sitter effect and frame-dragging around the earth are both of order ~10 milliarcsec/yr, so to measure either of them with 1% accuracy requires that all unmodeled precessions on this rotor (known technically as the "drift rate") add up to less than 0.1 milliarcsec/yr, or 10^-18 rad/s. (See video clip "How smalll is 1/10th of a milliarcsecond?" at right.)

What does this requirement mean for our gyroscope? Precession Ω is related to torque τ by Ω=τ/(Iω) where I = (2/5)mr² is the moment of inertia and ω=v/r is the angular velocity. Inhomogeneities of size δr produce torques of order τ=maδr where a is the tangential acceleration. Combining these expressions gives a drift rate of Ω = (5/2)(a/v)(δr/r). Assuming a spin speed of v~1000 cm/s and accelerations comparable to those on the surface of the earth (a~g), the rotor must be homogeneous to within (δr/r) <>-17 to attain a drift rate less than 10^-18 rad/s! Such homogeneities are utterly unattainable on earth. In space, however, it is possible — just possible, with a great deal of work — to suppress unwanted accelerations on a test body by as much as eleven orders of magnitude, to a~10^-11g. If this can be done, then the gyro rotor need only be homogeneous to one part in 10⁶, rather than 10¹⁷ — a level that can be achieved, with great effort, using the best materials on earth.

Considerations of this kind led two people to take a new look at gyroscopic tests of general relativity shortly after the dawn of the space age. George E. Pugh (b. 1928) and Leonard I. Schiff (1915-1971) hit independently on the key ideas within months of each other. Pugh was stimulated by a talk given by Huseyin Yilmaz proposing a satellite test to distinguish his alternative theory of gravity from Einstein's, while Schiff was likely inspired at least in part by an advertisement for a new "Cryogenic Gyro ... with the possibility of exceptionally low drift rates" in Physics Today magazine (see Francis Everitt's contribution to Near Zero: New Frontiers of Physics, 1988). Pugh's paper, published in a Pentagon memorandum in November 1959, is now recognized as the birth of the concept of drag-free motion. This is a critical element of the Gravity Probe B mission, whereby any one of the gyroscopes can be isolated from the rest of the experiment and protected from all non-inertial forces; the rest of the spacecraft is then made to "chase after" the reference gyro by means of helium boiloff vented through a revolutionary porous plug and specially designed thrusters. In this way unmodeled accelerations on all the gyros, such as those resulting from the effects of solar radiation pressure and atmospheric friction on the spacecraft, can be reduced from a~10^-8g to below 10^-11g as required. (See animation clip "Drag-Free Motion" below.)

Schiff ~1970

Blackett	Pugh in 2007 Drag-free motion

The drag-free control system is only one of the innovations that made Gravity Probe B possible. The experiment depends on monitoring the precession of near-perfect gyroscopes relative to a fixed reference direction such as the line of sight to a distant guide star. But how is one to find the spin axis of a perfectly spherical, perfectly homogeneous gyroscope suspended in vacuum? This is the "readout problem"; another, closely related problem is how to spin up such a gyroscope in the first place. Various possibilities were considered in the early days, until 1962 when Francis Everitt and William Fairbank hit on the idea of exploiting what had until then been a small but annoying source of unwanted torque in magnetically levitated gyroscopes. Spinning superconductors develop a magnetic moment, known as the London moment, which is proportional to spin speed and always aligned with the spin axis. If the rotors were levitated electrically instead of magnetically, this tiny effect could be used to tell where their spin axes were pointed. (Measuring it would of course require magnetic shielding orders of magnitude beyond anything available in 1962, another story in itself.) Thus was born the London moment readout, which in its modern incarnation uses SQUIDs (Superconducting QUantum Interference Devices) as magnetometers. So sensitive are these devices that they register a change in spin-axis direction of 1 milliarcsec in five hours of integration time. (See animation clip "London Moment Readout" below.)

	">
London Moment readout	Dan Debra, Bill Fairbank, Francis Everitt and Bob Cannon with a model of Gravity Probe B, 1980

These are only two pieces of an experiment so beautifully intricate that it is as much a work of art as it is science and technology. Many of its key features reflect a guiding principle of physics experimenters through the ages, namely to turn obstacles into opportunities. How, for instance, can one meaningfully compare the gyroscope spin-axis direction (which is read out in volts) with the position of the guide star (which comes from an onboard telescope in radians)? The answer is to exploit nature's own calibration in the form of stellar aberration. This phenomenon, an apparent back-and-forth motion of the guide star position due to the orbit of the earth around the sun, is entirely Newtonian and inserts "wiggles" into the data whose period and amplitude are exquisitely well known (to give a sense of the precision of the experiment, the calibration requires terms of second, as well as first order in the earth's speed v/c). What about the fact that the guide star has an unknown "proper motion" large enough to obscure the predicted relativity signal? This allows the experiment to be designed in a classic "double-blind" fashion; a separate team of astronomers uses VLBI (Very Long-Baseline radio Interferometry) to monitor the movements of the guide star itself, relative to even more distant quasars. Only at the conclusion of the experiment are the two sets of data to be compared; this helps to prevent the physicists from "finding what they want to see."

For many more such examples, see the Unique Technology Challenges & Solutions page in the Technology tab. Gravity Probe B (or the Stanford Relativity Gyroscope Experiment, as it was known until 1971) received its first NASA funding in March 1964. The photograph above shows several of the early project leaders with a model of the spacecraft circa 1980: Dan Debra (a propulsion expert), Fairbank (the experimental low-temperature physicist par excellence), Everitt and Bob Cannon (a gyroscope specialist). See the History & Management section of the Mission page for more details.

Back to Top

Astrophysical Significance

Radio image of the giant jet
in NGC 6251

Artist's depiction of a
supermassive black hole

When Gravity Probe B was originally conceived, frame-dragging was seen as being of more theoretical than practical interest. To be sure, experimental confirmation of the Einstein (i.e. Lense-Thirring) prediction would place another independent constraint on alternative metric theories of gravity. Frame-dragging precession is proportional to the combination of PPN parameters (γ+1+α₁/4)/2 where γ describes the warping of space and α₁ is known as a "preferred-frame" parameter that allows for a possible dependence on motion relative to the rest frame of the universe (it takes the value zero in general relativity). However, frame-dragging is such a small effect in the solar system that experimental bounds it places on these parameters are not likely to be competitive with those from other tests. Confirmation of the Einstein (i.e. Lense-Thirring) prediction at the 1% level, for example, would translate into a comparable bound on γ and would not significantly constrain α₁.

Bardeen-Petterson effect

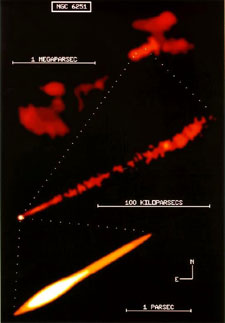
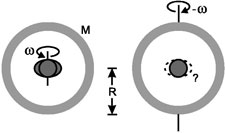
This situation has changed dramatically since the 1980s. Physicists now see frame-dragging as the gravitational analog of magnetism, and astrophysicists invoke this gravitomagnetic field as the engine and alignment mechanism for the vast and otherwise incomprehensible jets of gas and magnetic field ejected from quasars and galactic nuclei like the radio source NGC 6251, as shown above left. We know that these jets act as power sources for quasars and other strong extragalactic radio sources and that they are generated by compact, supermassive objects (almost certainly black holes) inside galactic nuclei, as illustrated above right. The megaparsec distance scale in the radio image above left implies that these compact objects are capable of holding the jet direction constant over timescale as long as ten million years. Black holes can only do this by means of their gyroscopic spin, and they can only communicate the direction of that spin to the jet via their gravitomagnetic field H. Such a field will cause an accretion disk to precess around the black hole, and that precession combined with the disk's viscosity should drive the inner region of the disk into the hole's equatorial plane, resulting in only two preferred directions for the jets: the north and south poles of the black hole. This phenomenon, known as the Bardeen-Petterson effect (diagram at left), is widely believed to be the physical mechanism responsible for jet alignment.

Blandford-Znajek effect

Kip Thorne discusses black holes
in the context of GP-B

Gravitomagnetism is also thought to explain the generation of the astounding energy contained in these jets in the first place. The event horizon of the black hole acts like a "gravitomagnetic battery", driving currents around closed loops like that shown in the diagram at left: up the magnetic field lines from the horizon to a region where the magnetic field is weak, across the field lines there, and then back down the field lines to the horizon and through the "battery" where the gravitomagnetic potential of the black hole interacts with the tangential component of the ordinary magnetic field B to produce a drop in electric potential (see Kip Thorne's contribution to Near Zero: New Frontiers of Physics, 1988). This phenomenon, known as the Blandford-Znajek mechanism, effectively draws on the immense gravitomagnetic, rotational energy of the supermassive black hole and converts it into an outgoing stream of ultra-relativistic charged particles. Gravity Probe B has thus become a crucial test of the mechanism that powers the most violent explosions in the universe.

Back to Top

Cosmological Significance

Star trails at night

Here is a simple experiment that almost anyone can perform on a clear night: pirouette freely around while looking up at the stars. You will notice two things: one, that the stars seem to spin around in the sky, and two, that your arms are pulled upwards by centrifugal force. Are these phenomena connected in some physical way? Not according to Newton. For him, centrifugal force is a consequence of accelerating (i.e. rotating) with respect to absolute space; it has no physical origin (and is therefore often called a "fictitious force" in elementary physics classes). It is, furthermore, a coincidence that the stars above us are at rest with respect to this same absolute space. We look upward, in effect, from two fundamentally different reference frames: one defined by our local sense of inertia, and the other defined by the global rest frame of the universe at large. Why should these two reference frames happen to coincide? Newton did not try to answer this question.

Kip Thorne discusses the significance
of GP-B for astrophysics & cosmology

We know that the concept of absolute space(time) is retained in general relativity, so we might have expected that the same coincidental alignment of our local inertial frame with that of the global matter distribution would carry over to Einstein's theory as well. Astonishingly, however, it does not. If general relativity is correct, then there are strong indications that our local "compass of inertia" has no choice but to be aligned with the rest of the universe — the two are linked by the frame-dragging effect. These indications do not come from experiment, but from theoretical calculations similar to that performed by Lense and Thirring. The calculations show that general-relativistic frame-dragging goes over to "perfect dragging" when the dimensions of the large mass (its size and density) become cosmological. In this limit, the distribution of matter in the universe appears sufficient to define the inertial reference frame of observers within it. For a particularly clear and simple explanation of how and why this happens, see The Unity of the Universe (1959) by Dennis Sciama. Had Mach lived 10 years longer, he could have predicted the existence of the extragalactic universe based on observations that the stars in the Milky Way rotate around a common center!

Would the earth still bulge, if it were
standing still and the universe were
rotating around it?

To put the cosmological significance of frame-dragging in concrete terms, imagine that the earth were standing still and that the rest of the universe were rotating around it: would its equator still bulge? Newton would have said "No". According to standard textbook physics the equatorial bulge is due to the rotation of the earth with respect to absolute space. On the basis of Lense and Thirring's results, however, Einstein would have had to answer "Yes"! In this respect general relativity is indeed more relativistic than its predecessors: it does not matter whether we choose to regard the earth as rotating and the heavens fixed, or the other way around: the two situations are now dynamically, as well as kinematically equivalent. The early calculations were flawed in many ways, but the phenomenon of perfect dragging has persisted in most subsequent, more sophisticated treatments, notably those of Helmut Hönl and Heinz Dehnen (1962, 1964), Dieter Brill and Jeffrey Cohen (1966) and Herbert Pfister and Karlheinz Braun (1986). Pfister sums up current thinking this way in Mach's Principle: From Newton's Bucket to Quantum Gravity (1995): "Although Einstein's theory of gravity does not, despite its name 'general relativity,' yet fulfil Mach's postulate of a description of nature with only relative concepts, it is quite successful in providing an intimate connection between inertial properties and matter, at least in a class of not too unrealistic models for our universe. Perhaps against majority expectation, this connection is instantaneous in nature. Furthermore, general relativity has brought us nearer to an understanding of the observational fact that the local inertial compass is fixed relative to the most distant cosmic objects, but there is surely desire for still deeper understanding." Thus does direct detection of frame-dragging by Gravity Probe B gain new importance: it will shine experimental light on what has heretofore been a theoretical mystery, namely the origin of inertia. For some, this is perhaps the most beautiful and profound manifestation of spin in Einstein's spacetime: it binds us here to the universe out there, in such a way that you, standing at night under the stars on a planet known as earth, cannot turn so much as around without feeling a tug from the rest of the universe.

Original here

Astronomy Picture of the Day

Discover the cosmos! Each day a different image or photograph of our fascinating universe is featured, along with a brief explanation written by a professional astronomer.

2008 May 11

Retrograde Mars
Credit & Copyright: Tunç Tezel (TWAN)

Explanation: Why would Mars appear to move backwards? Most of the time, the apparent motion of Mars in Earth's sky is in one direction, slow but steady in front of the far distant stars. About every two years, however, the Earth passes Mars as they orbit around the Sun. During the most recent such pass over the last year, the proximity of Mars made the red planet appear larger and brighter than usual. Also during this time, Mars appeared to move backwards in the sky, a phenomenon called retrograde motion. Pictured above is a series of images digitally stacked so that all of the stars images coincide. Here, Mars appears to trace out a loop in the sky. Near the top of the loop, Earth passed Mars and the retrograde motion was the highest. Retrograde motion can also be seen for other Solar System planets.

Original here

UFOh noes!

I got an email from writer Paul McNamara about my recent comments complaining about shoddy journalism when it comes to UFO reports. Turns out he wrote a list of 10 reasons not to believe in UFOs, and while it’s a tad snarky it really hits the high notes.

To his list, I’ll add my #1 reason of all time: why don’t amateur astronomers report them in record numbers? After all, who spends more time looking at the sky? The fact that few if any amateurs report them is a pretty clear case that the vast majority, at least, of all UFO reports are misunderstood mundane objects like airplanes, satellites, reflections, meteors, and Venus. Sometimes even the Moon, amazingly.

When a flying saucer lands on the White House lawn, someone call me.

Original here

A New Approach to Treating Alzheimer's

Stimulating memories: Scientists are testing electrical stimulation of the hypothalamus, shown here in green, as a novel treatment for Alzheimer’s disease. The hypothalamus lies adjacent to the fornix, a crucial part of the brain’s memory circuit. Credit: Scott Camazine & Sue Trainor / Photo Researchers, Inc

Earlier this year, neurosurgeon Andres Lozano published a startling finding. He was testing deep-brain stimulation, in which electrical current is delivered directly to the brain, as a treatment for obesity. The patient's weight showed little change, but his memory improved significantly. Lozano has now formed a company to commercialize the technique as an Alzheimer's therapy, and he's testing it in six patients in the early stages of the disease.

Alzheimer's is sorely in need of new treatment approaches. Five million people suffer from it in the United States, a number expected to rise dramatically as the baby boomers enter their senior years. Finding new treatments has proved extremely difficult: drugs currently on the market have at best only a modest impact on symptoms. And experimental drugs that improve cognitive function in animals have largely failed in human tests.

In the past few years, deep-brain stimulation has become a routine treatment for Parkinson's disease: approximately 40,000 patients worldwide have undergone the procedure. Scientists are now testing it as a way to treat a growing number of other disorders, including epilepsy, depression, and obsessive-compulsive disorder.

In the procedure, a thin electrode is surgically implanted into part of the brain, stimulating neurons in brain areas affected by disease. The voltage delivered to the brain is controlled by a power pack implanted in the patient's chest and connected to the electrode via wires threaded beneath the skin.

The patient whose obesity Lozano was attempting to treat is cognitively normal. Lozano's team found that turning on the electrical stimulation triggered old memories in the patient; the higher the voltage, the more details he recalled. More important, after several months of low-level stimulation, cognitive testing revealed that the man's memory significantly improved. "Verbal working memory went off the scale," says Lozano, who holds a Canada Research Chair in Neuroscience at the University of Toronto, in Canada. "We've shown that the function of memory circuits can be modulated."

With Alzheimer's, a neurodegenerative disease that affects brain cells involved in memory, the idea is to boost activity in the memory circuits that patients have left. Lozano's group is targeting the fornix, which he describes as a highway that drives information to and from the brain's memory center, the hippocampus. (The electrode is actually implanted into the neighboring hypothalamus, which was selected for the obesity patient because of its role in controlling appetite. But brain-imaging studies confirm that stimulation triggers activity in the neural circuit that encompasses the fornix and the hippocampus.)

Lozano and his collaborators have seen promising results in the six patients in their trial: turning on the stimulation boosts cognitive function. Lozano now aims to begin larger clinical trials. It's not yet clear how the therapy will fare in the long run. While deep-brain stimulation's success in treating Parkinson's, which is also a neurodegenerative disease, provides some encouragement, other human studies of Alzheimer's therapies that yielded promising early results failed to show effectiveness in later tests.

The researchers are performing parallel experiments in rats and have found that electrical stimulation can drive production of new memories and boost production of new brain cells, which may also boost memory function.

Original here

Dissolving Dead Bodies: Gross, But Green

The New Green Funeral?

Since they first walked the planet, humans have either buried or burned their dead. Now a new option is generating interest -- dissolving bodies in lye and flushing the brownish, syrupy residue down the drain.

The process is called alkaline hydrolysis and was developed in this country 16 years ago to get rid of animal carcasses. It uses lye, 300-degree heat and 60 pounds of pressure per square inch to destroy bodies in big stainless-steel cylinders that are similar to pressure cookers.

No funeral homes in the United States -- or anywhere else in the world, as far as the equipment manufacturer knows -- offer it. In fact, only two U.S. medical centers use it on human bodies, and only on cadavers donated for research.

But because of its environmental advantages, some in the funeral industry say it could someday rival burial and cremation.

"It's not often that a truly game-changing technology comes along in the funeral service," the newsletter Funeral Service Insider said in September. But "we might have gotten a hold of one."

Getting the public to accept a process that strikes some as ghastly may be the biggest challenge. Psychopaths and dictators have used acid or lye to torture or erase their victims, and legislation to make alkaline hydrolysis available to the public in New York state was branded "Hannibal Lecter's bill" in a play on the sponsor's name -- Sen. Kemp Hannon -- and the movie character's sadism.

Alkaline hydrolysis is legal in Minnesota and in New Hampshire, where a Manchester funeral director is pushing to offer it. But he has yet to line up the necessary regulatory approvals, and some New Hampshire lawmakers want to repeal the little-noticed 2006 state law legalizing it.

"We believe this process, which enables a portion of human remains to be flushed down a drain, to be undignified," said Patrick McGee, a spokesman for the Roman Catholic Diocese of Manchester.

State Rep. Barbara French said she, for one, might choose alkaline hydrolysis.

"I'm getting near that age and thought about cremation, but this is equally as good and less of an environmental problem," the 81-year-old lawmaker said. "It doesn't bother me any more than being burned up. Cremation, you're burned up. I've thought about it, but I'm dead."

In addition to the liquid, the process leaves a dry bone residue similar in appearance and volume to cremated remains. It could be returned to the family in an urn or buried in a cemetery.

The coffee-colored liquid has the consistency of motor oil and a strong ammonia smell. But proponents say it is sterile and can, in most cases, be safely poured down the drain, provided the operation has the necessary permits.

Alkaline hydrolysis doesn't take up as much space in cemeteries as burial. And the process could ease concerns about crematorium emissions, including carbon dioxide as well as mercury from silver dental fillings.

The University of Florida in Gainesville and the Mayo Clinic in Rochester, Minn., have used alkaline hydrolysis to dispose of cadavers since the mid-1990s and 2005, respectively.

Brad Crain, president of BioSafe Engineering, the Brownsburg, Ind., company that makes the steel cylinders, estimated 40 to 50 other facilities use them on human medical waste, animal carcasses or both. The users include veterinary schools, universities, pharmaceutical companies and the U.S. government.

Liquid waste from cadavers goes down the drain at the both the Mayo Clinic and the University of Florida, as does the liquid residue from human tissue and animal carcasses at alkaline hydrolysis sites elsewhere.

Manchester funeral director Chad Corbin wants to operate a $300,000 cylinder in New Hampshire. He said that an alkaline hydrolysis operation is more expensive to set up than a crematorium but that he would charge customers about as much as he would for cremation.

George Carlson, an industrial-waste manager for the New Hampshire Department of Environmental Services, said things the public might find more troubling routinely flow into sewage treatment plants in the United States all the time. That includes blood and spillover embalming fluid from funeral homes.

The department issued a permit to Corbin last year, but he let the deal on the property fall through because of delays in getting the other necessary permits. Now he must go through the process all over again, and there is gathering resistance. But he said he is undeterred.

"I don't know how long it will take," he said recently, "but eventually it will happen."

Original here

Scientist team creates first GM human embryo

Scientists have created what is believed to be the first genetically modified (GM) human embryo.

A team from Cornell University in New York produced the GM embryo to study how early cells and diseases develop. It was destroyed after five days.

The British regulator, the Human Fertilisation and Embryology Authority (HFEA), has warned that such controversial experiments cause “large ethical and public interest issues”.

News of the development comes days before MPs are to debate legislation that would allow scientists to use similar techniques in this country.

The effects of changing an embryo would be permanent. Genes added to embryos or reproductive cells, such as sperm, will affect all cells in the body and will be passed on to future generations.

The technology could potentially be used to correct genes which cause diseases such as cystic fibrosis, haemophilia and even cancer. In theory, any gene that has been identified could be added to embryos.

Ethicists warn that genetically modifying embryos could lead to the addition of genes for desirable traits such as height, intelligence and hair colour.

The Human Fertilisation and Embryology Bill, which will have its second reading this week, will make it legal to create GM embryos in Britain.

The bill will allow GM embryos to be created only for research and will ban implantation in the womb. Ethicists, however, say that the legislation could be relaxed in the future.

The HFEA has said that it is preparing for scientists to apply for licences to create GM embryos. A paper, published by the authority, states: “The bill has taken away all inhibitions on genetically altering human embryos for research. The Science and Clinical Advances Group [of the HFEA] thought there were large ethical and public interest issues and that these should be referred for debate.”

The Cornell team, led by Nikica Zaninovic, used a virus to add a gene, a green fluorescent protein, to an embryo left over from in vitro fertilisation.

The research was presented at a meeting of the American Society of Reproductive Medicine last year but details have emerged only after the HFEA highlighted the work in a review of the technology.

Zaninovic pointed out that in order to be sure that the new gene had been inserted and the embryo had been genetically modified, scientists would ideally need to grow the embryo and carry out further tests.

The Cornell team did not have permission to allow the embryo to progress, however.

Scientists argue that the embryos could be used to study how diseases develop. They also say GM embryos could be more efficient in generating stem cells.

However, Dr David King, director of Human Genetics Alert, warned: “This is the first step on the road that will lead to the nightmare of designer babies and a new eugenics. The HFEA is right to say that the creation and legalisation of GM embryos raises ‘large ethical and public interest issues’ but neglects to mention that these have not been debated at all.”

He added: “I have been speaking to MPs all week and no one knows that the government is legalising GM embryos. The public has had enough of scientists sneaking these things through and then presenting us with a fait accompli.”

Original here

Rats feel peer pressure too

It's not just humans who succumb to peer pressure - rats do too. Brown rats have a tendency to disregard personal experiences and copy the behaviour of their peers. What's more, the urge to conform appears to be so strong that they will choose to eat food they know to be unpalatable when interacting with other rats that have done the same.

Bennett Galef and Elaine Whiskin at McMaster University in Hamilton, Ontaria, Canada, put rats off cinnamon-flavoured food pellets by injecting the animals with a nausea-inducing chemical after their meals. Given a choice, these trained animals preferred to eat cocoa-flavoured food pellets.

However, when those rats then spent time with "demonstrator" rats that had just eaten and smelt of cinnamon, they regained their liking for it (Animal Behaviour, DOI: 10.1016/j.anbehav.2007.11.012).

Until now, humans and chimps were the only other animals known to conform in this way. Andrew Whiten from the University of St Andrews, UK, says that the discovery emphasises the importance of social learning in the animal kingdom.

The big question now, he says, is why they conform. "It's not immediately obvious why a rat or chimp or human would cast aside what it knows from its own experience and adopt an inferior course of action just because everybody else is doing it."

Original here

Why Emotional Memories Of Traumatic Life Events Are So Persistent

Following co-presentation with nausea, conditioned mice avoid the sugar solution for months. (Credit: Image courtesy of ETH Zurich)

Emotional memories of traumatic life events such as accidents, war experiences or serious illnesses are stored in a particularly robust way by the brain. This renders effective treatment very difficult. Researchers at ETH Zurich and the University of Zurich have now successfully tracked down the molecular bases of these strong, very persistent memories.

The expression “post-traumatic stress disorder” is once again constantly on everyone’s lips in relation to those returning from the Iraq war or survivors of catastrophes such as the tsunami. This is not a new development, since it always occurs when people experience extreme situations. It is known that emotional memories of both a positive and a negative kind are stored by our brain in a particularly robust way.

Consequently they have a very large effect on our behaviour and, in the case of adverse memories, they can place considerable restrictions on the way we go about our lives. As a result, we avoid places, smells or objects that remind us of the traumatic experience, because they may trigger severe anxieties. Isabelle Mansuy, Professor of Cellular Neurobiology at ETH Zurich and of Molecular and Cognitive Neurosciences at the University of Zurich, and her research group have now shown that the enzyme calcineurin and the gene regulation factor Zif268 decisively determine the intensity of emotional memories. For the first time, this has enabled the regulatory processes at the synapse, which are important for emotional memories, to be linked to the processes in the cell nucleus.

Mice as an ideal model system

The generation of very persistent memories in the shortest possible time needs molecules in the brain that are not only activated rapidly but which also efficiently control the signalling pathways of long-term information storage in the brain. This is why the protein phosphatase calcineurin, which was already known to have a negative regulatory effect on learning and memory, was a very promising candidate for the Zurich researchers. The researchers used mice as the model system because their learning processes are very similar to those in humans, and established behavioural tests already exist. In their experiments, the researchers conditioned the mice to associate a sugar solution with nausea. This association persists for many months. The mice avoid the sugar solution during this period.

However, their aversion can be overcome slowly through intensive training. Mansuy explains that “Emotional memories are not simply erased. Oppressive negative memories need to be actively replaced by positive memories.” She says it is important at the same time to understand that the negative memories do not disappear, they merely slide down in a kind of priority list and are outweighed by the newly learned positive memories. Mansuy says “This process is not final and absolute, since the priority list can change again.” Karsten Baumgärtel, a post-doctoral researcher in Mansuy’s group, stresses that this is a big difference between emotional memories and learned knowledge. “It is entirely possible for facts to vanish completely from the memory, whereas in extreme cases emotional recollections remain stored for a whole lifetime. Active intervention is necessary to reduce the priority level of negative memories.”

Reduced calcineurin activity

Studies of the amygdala, that part of the brain which is important for emotional perception, showed reduced activity of the enzyme calcineurin in conditioned mice compared to mice in which no association with nausea had been generated. Because calcineurin is a negative regulator of learning and memory, its activity needs to be reduced to enable strong memorisation. To gain more evidence about the role of calcineurin in the memory process, the researchers used transgenic mice in which they were able to selectively activate or deactivate the enzyme in nerve cells of the brain. Mansuy explains that “This selective activation and inactivation in nerve cells is important because calcineurin is an enzyme that occurs in many cells.

For example it also plays an important part in the immune defence system.” As the researchers expected, inactivating calcineurin strengthened the memory of the association between sugar solution and nausea, whereas the memory was weakened by increased calcineurin activity. The researchers were also able to demonstrate that the period of time needed to suppress the negative memory by a purely positive memory could be prolonged or shortened respectively by this intervention.

Regulation processes in synapses and the cell nucleus

Inactivating calcineurin also causes increased expression of the gene regulator Zif268 in the amygdala. Zif268 is responsible for regulating a wide variety of important genes that play a role in the signal processing of memories and learning. Simulating this increased expression of Zif268 in transgenic mice intensified memory in a similar way to the inactivation of calcineurin. This is the first occasion on which it has been possible to demonstrate this magnitude of functional relationship between the activity of an enzyme in the synapse and that of a gene regulation factor in the cell nucleus.

Mansuy and Baumgärtel stress that the purpose of their research is to gain a fundamental understanding of the molecular relationships, but that it is not associated in any way with a direct clinical application in the near future. However, Mansuy explains that: “In the past, the origin of many diseases was unknown and they were regarded as a punishment from God, and at that time those who were affected went to the priest. Nowadays we understand the mechanisms underlying them and can treat these illnesses. We hope that our research has made a small contribution to enabling the same situation also to apply in the future to psychological traumas or brain diseases with memory weakness such as Alzheimer’s, Parkinson’s and strokes.”

Original here

Pavlov's Bacteria?

Prognosticator.
E. coli may be able to predict an upcoming oxygen deficit based on temperature cues.

We've all heard of Pavlov's dogs, the famous canines trained by Russian physiologist Ivan Pavlov to associate food with the sound of a bell. Now, scientists have found that bacteria may be capable of similar behavior--an ability never seen in such simple organisms.

Researchers already know that microbes can mount simple responses to changes in their environment, such as acidity fluctuations, by altering their internal workings. If the changes are regular enough, bacteria can respond ahead of time. But systems biologist Saeed Tavazoie of Princeton University wondered if microbes were capable of more sophisticated reasoning. Could they, for example, learn to match a signal that didn't occur regularly to a probable future event? If so, the bacterium could improve its chances of survival by turning on a preemptive response to that event.

Tavazoie and colleagues first ran a computer simulation to determine if a simple system could evolve such behavior. They created an environment inhabited by evolving virtual bugs. The organisms garnered more energy if they could "learn" that certain signals preceded the arrival of food and launch a preemptive metabolic response. Even when the signal combinations grew more complex, the population was able to evolve the correct responses, the team reports online this week in Science.

The researchers then looked for evidence of this ability in the bacterium Escherichia coli. Because E. coli gets warmer when it enters a human mouth--ferried in on some old meatloaf, perhaps--and then must soon contend with low oxygen levels as it passes into the large intestine, the team reasoned that the bacterium might use temperature as a cue to prepare for the upcoming lack of oxygen. Indeed, when the researchers turned up the heat in a dish of E. coli, the bugs dialed down activity in genes that normally operate in high-oxygen conditions. But the true test came when the team flipped the normal association, growing the bacteria in conditions in which high oxygen levels followed temperature increases. Less than 100 generations later, the bacteria stopped turning on their low-oxygen response after exposure to high temperatures, suggesting that they had evolved to break the association.

The study is the "first convincing demonstration" that bacteria can use environmental cues to anticipate events, says Michael Travisano, an evolutionary biologist at the University of Minnesota, Twin Cities. The work could open up new ways to explain puzzling behavior of microbial pathogens, which might use predictive signals to change their cell surfaces and avoid a host's impending immune attack. "If it does something you don't understand, maybe it's anticipating an environmental shift," he says.

Original here

Scientists dig deeper into the genetics of schizophrenia by evaluating microRNAs

Shown here is human chromosome 22 and the piece of the chromosome missing in some patients with schizophrenia. Loss of this chromosomal piece (22q11) is the only known recurrent copy number mutation associated with schizophrenia. The corresponding region on mouse chromosome 16 is indicated along with the position of the engineered deletion in the mouse model. The engineered deletion results in alterations in microRNA production and as a result neuronal and behavioral deficits. © 2008 Columbia University

Researchers at Columbia University Medical Center have illuminated a window into how abnormalities in microRNAs, a family of molecules that regulate expression of numerous genes, may contribute to the behavioral and neuronal deficits associated with schizophrenia and possibly other brain disorders.

In the May 11 issue of Nature Genetics, Maria Karayiorgou, M.D., professor of psychiatry, and Joseph A. Gogos, M.D., Ph.D., associate professor of physiology and neuroscience at Columbia University Medical Center explain how they uncovered a previously unknown alteration in the production of microRNAs of a mouse modeled to have the same chromosome 22q11.2 deletions previously identified in humans with schizophrenia.

“We’ve known for some time that individuals with 22q11.2 microdeletions are at high risk of developing schizophrenia,” said Karayiorgou, who was instrumental in identifying deletions of 22q11.2 as a primary risk factor for schizophrenia in humans several years earlier. “By digging further into this chromosome, we have been able to see at the gene expression level that abnormalities in microRNAs can be linked to the behavioral and cognitive deficits associated with the disease.”

The investigators modeled mice to have the same genetic deletion as the one observed in some individuals with schizophrenia and examined what happens in the expression of over 30,000 genes in specific areas of the brain. When they discovered that the gene family of microRNAs was affected, they suspected that the Dgcr8 gene was responsible. The Dgcr8 gene is one of the 27 included in the 22q11.2 microdeletion and has a critical role in microRNA production, so this was a logical hypothesis. Indeed, when they produced a mouse deficient for the Dgcr8 gene, and tested it on a variety of cognitive, behavioral and neuroanatomical tests, they observed the same deficits often observed in people with schizophrenia.

“Our studies show that alterations in microRNA processing result in synaptic and behavioral deficits,” said Dr. Gogos. Drs. Karayiorgou and Gogos have partnered together to decipher the role of individual genes from 22q11 in the development of schizophrenia by using human genetics and animal model approaches.
The significance of this work is that it implicates a completely novel, previously unsuspected group of susceptibility genes and brings investigators a step closer to understanding the biological mechanisms of this disorder. Implication of such a large family of genes (the most recent estimate puts the number of human microRNAs at at least 400 that influence the expression of as many as a third of all genes) could partly account for the genetic complexity associated with this devastating disorder and explain some of the difficulties that the researchers have encountered in their efforts to pinpoint individual genes.

“Our hope is that the more we know about the genes involved in schizophrenia, the more targeted treatment can be,” said Dr. Gogos.

“Much in the way that cancer patients who have tested for a particular gene, such as BRAC1, can be tested and then treated with protocols designed specifically for them, we want to be able to know enough about the schizophrenic brain to target treatments to individual patients.”

The next step for the researchers is to find the many genes whose expression is controlled by the identified deficient microRNAs, which could in turn be involved in the pathogenesis of schizophrenia. Much more study and identification of other genetic variants must be done to further illuminate the disease’s genetic underpinnings, according to Drs. Karayiorgou and Gogos.

Original here

Stephen Hawking in hunt for Africa's hidden talent

Professor Stephen Hawking, who has devoted his career to finding the origins of the universe, is to begin a new search – for Africa’s answer to Einstein.

Despite suffering from motor neurone disease which has left him almost completely paralysed, Hawking, 66, has made the journey to South Africa to launch the project today.

Some of the world’s leading high-tech entrepreneurs and scientists have backed the £75m plan to create Africa’s first postgraduate centres for advanced maths and physics, after the British government declined to provide funding.

Hawking will be joined by eminent physicists and mathematicians including two Nobel laureates in physics, David Gross and George Smoot, and Michael Griffin, the head of Nasa. Naledi Pandor, South Africa’s education minister, will also speak.

“The world of science needs Africa’s brilliant talents and I look forward to meeting prospective young Einsteins from Africa,” said Hawking.

Neil Turok, founder of the project and professor of mathematical physics at Cambridge University, where he is a close colleague of Hawking, said the aim of the centres was to “unlock and nurture scientific talent” across Africa. “Apart from an African Einstein, we want to find the African Bill Gates and the Sergey Brins and Larry Pages of the future,” said Turok, referring to the founders of Microsoft and Google.

The 15 new centres will be modelled on the African Institute for Mathematical Sciences (Aims) which was founded by Turok in Muizenberg, near Cape Town, four years ago. It has produced 160 graduates from 30 African countries, many of whom have gone on to take science doctorates. Another 53 will graduate shortly.

Among them is Buthaina Adam, whose mathematical skills shone out in Sudan’s war-torn Darfur province where she grew up. With a physics degree from the University of Khartoum, she hoped to become a nuclear physicist, but shortage of money and opportunities left her career on hold until she was offered a place at Aims in 2006.

“Aims gave me a life, opened doors for me,” said Adam, who hopes to return to Darfur and teach after completing a PhD.

Turok decided to push for 15 more Aims institutes after winning the £50,000 Technology, Entertainment and Design prize in America earlier this year. He donated the money to Aims.

He has since been offered support potentially worth tens of millions of pounds. Google, the Gates Foundation and Sun Microsystems are among those that have expressed interest.

Turok and Hawking hope that Aims’s students will help to overturn the negative stereotypes of Africa that were recently given expression by James Watson, the co-discoverer of DNA.

Watson lost his job as director of the Cold Spring Harbor laboratories in America after suggesting that Africans were less intelligent than Europeans. A subsequent analysis of his own DNA showed that he had part-African ancestry.

“Watson’s views were simply ridiculous,” said Turok. “The quality of students we are seeing at Aims is extremely high. What they need is an opportunity to learn.”

Hawking’s keynote lecture this afternoon is expected to be the highpoint of the ceremonies in Cape Town. When he gave a talk at the Caltech campus in Pasadena in the United States, he was wheeled out of the auditorium to a standing ovation and took a victory lap in his wheel-chair while the crowd shouted: “We love you, Stephen.”

Hawking is expected to repeat his call for a global effort to enable humanity to colonise space, starting with the moon and then Mars. Turok’s hopes are more down to earth: he wants to persuade the British government to rethink its refusal to fund the Aims project.

“The Department for International Development spends £1.5 billion of taxpayers’ money on aid to Africa every year but there is precious little to show for it. The people who will make Africa rich are the brightest people because they will generate wealth,” Turok said.

Andrew Mitchell, shadow development secretary, was equally critical: “There is much more to Africa than poverty and starvation. This is an extremely important initiative and I’m going to see how the next Conservative government could support it.”

The international development department said it preferred to focus on projects to fight poverty.

Original here

The World's Spookiest Weapons

Cyborg animals, psychotropics and flying lasers are just some of the terrifying weapons government labs have cooked up over the years

Terrifying Weapons: Mushroom cloud from the 1970 French Polynesian Licorne test.

View Photo Gallery

Atom bombs are just the beginning. In the last half-century, the greatest military minds on Earth have developed an arsenal of weapons to make mutually assured destruction seem tame.

Whether these masterpieces of destruction come from miles above Earth or millimeters below the skin, they have one thing in common: they're spooky as hell.

Can turning animals into cyborgs ever end well? Should lasers really be strapped to planes? Is dispersing humans with the worst smell ever created a better alternative to doing it by burning their skin? You be the judge. Launch our gallery of the world's spookiest weapons—some decades away and others already implemented—and marvel over what humans can create when they work apart.

Original here

Lasers May Treat Cancers of the Larynx

For people with early cancer of the larynx, the standard treatment can be grueling: a biopsy in an operating room followed by a six-week course of radiation that may lead to permanent hoarseness or speech impairment.

The New York Times

But a team of Harvard doctors is reporting that a new outpatient laser procedure promises to eliminate the need for radiation, preserve speech, shorten treatment time and significantly improve care in other ways for many patients whose cancer is diagnosed early.

The therapy, which uses heat from the laser to destroy the tumor’s blood supply and cancer cells, damages surrounding tissue far less than radiation and different types of lasers.

It has been tested in only 28 patients, all at Massachusetts General Hospital in Boston. Yet the initial findings hold promise because the laser was the patients’ only treatment and none have had a recurrence or needed surgery or radiation after a mean follow-up of 27 months, the team’s leader, Dr. Steven M. Zeitels, said in an interview. The longest is more than five years.

Other experts expressed cautious optimism about the findings from the pilot study, which the Harvard team reported May 1 at a meeting of the American Broncho-Esophagological Association in Orlando. The scientific report involved the first 22 of the 28 patients.

The procedure “represents a radically new approach to treatment of these cancers,” said Dr. Gregory A. Grillone, an otolaryngologist at Boston University School of Medicine. Dr. Grillone, who directs the Center for Voice and Swallowing at Boston Medical Center, spoke in an interview after hearing Dr. Zeitels’s presentation at the meeting.

Dr. Zeitels agreed with Dr. Grillone and other experts who said the procedure must now be tested on more patients in other hospitals and monitored for a longer period before it could become a standard therapy. Longer studies comparing the new technique with standard therapy are needed to confirm that it is equally effective in curing the cancers.

Even then, only an estimated 2,000 of the 11,300 people, mostly men, who develop laryngeal cancer in this country each year seem likely to be candidates for the laser therapy.

Those eligible would be patients whose cancer was detected when the malignant growth was small and limited to one or both vocal cords in a form known as glottal cancer, which accounts for about 65 percent of new laryngeal cancers. An estimated one-third of glottal tumors are detected in an early stage, Dr. Zeitels said.

If studies confirm the early findings, then researchers must determine which kinds of laryngeal cancers and which patients are appropriate for the laser treatment, said Dr. Andrew Blitzer, a professor of otolaryngology at Columbia and director of the New York Center for Voice and Swallowing Disorders.

The initial clue to cancer of the vocal cords is often persistent hoarseness. The cancer most commonly develops among smokers, who are prone to developing additional types of cancer in the head and neck.

When radiation is used for laryngeal cancer, it cannot ordinarily be used again if other cancers develop nearby. So the laser procedure offers a strong additional advantage, Dr. Zeitels said — preserving radiation as a treatment option for laryngeal cancer patients who later develop head and neck cancers.

Treatment for laryngeal cancer has progressed slowly. Surgery was the only treatment until the advent of radiation in the early 20th century. In 1971, lasers began to be used for a noncancerous vocal cord problem, and different kinds of lasers have followed for vocal cord cancer.

The concept of the laser therapy derives from the work of the late Dr. Judah Folkman, the pioneering Harvard scientist who theorized that tumors could be starved by stopping angiogenesis — the process by which tumors stimulate formation of new blood vessels to feed themselves.

The new procedure relies on a type of laser called the pulsed photoangiolytic KTP. Its green light selectively destroys the blood vessels feeding the tumor without burning the vocal cords. “It’s like sandblasting the surface with light,” Dr. Zeitels said.

Vibration of the vocal cords is essential for good voice and speech. By preserving vocal cord function, the laser treatment allows the cords to vibrate, “not perfectly, but substantially better” than before patients had the procedure, Dr. Zeitels said.

“All the prior laser treatments would burn the vocal cords,” he said, “and when that happens they do not vibrate normally.”

Dr. Zeitels said his team had long used pulsed angiolytic lasers for a variety of benign laryngeal problems, including a precancerous condition called dysplasia.

The pulsed angiolytic laser has allowed ear, nose and throat specialists to treat most laryngeal dysplasias under local anesthesia in an office instead of general anesthesia in an operating room.

But “treating cancer is not the same as treating dysplasia,” he said, and he moved cautiously before using the laser for cancer.

One step was to alter the KTP laser to deliver the light in pulses to the soft tissue of the vocal cords, allowing the tissue to cool between bursts. The cooling prevented significant heat-induced scarring.

The first patient was John Ward, a professor at the Kellogg School of Management at Northwestern University. After several years in which he was hoarse and needed a microphone to give lectures, he said in a recent interview, doctors detected cancers on both vocal cords.

Dr. Ward read up on the disease and consulted with Dr. Zeitels and other specialists about his treatment options. Dr. Zeitels suggested the new laser therapy in extensive discussions, and Dr. Ward agreed.

The two tumors differed in size, so Dr. Zeitels said he aimed at preventing scars that might fuse the cords. He treated the larger cancer with a carbon dioxide laser and the smaller one with the angiolytic laser.

Six weeks later, both tumors had disappeared.

Dr. Ward said the treatment had saved his career — that he now had about 80 percent of his original quality of voice and 90 percent of its strength, and no longer needed a microphone to lecture.

Typically, patients are treated two to three times spaced six weeks apart to reduce the tumor’s size, Dr. Zeitels said. He added that it was generally safe to leave early vocal cord cancers in place for that period of time because they rarely spread at this stage.

Standard acoustic and other tests are performed in a sound-treated room before the procedure and monitored thereafter.

Urologists have used angiolytic lasers in a different way to burn prostate tissue, Dr. Zeitels said. For the vocal cords, “the procedure is dead-on easy” and could be performed by any ear, nose and throat specialist who learns to use the $70,000 laser, he said.

He also speculated that the angiolytic laser might eventually be adapted for treatment of cancers of the esophagus, bladder, cervix, windpipe and parts of the lungs.

Dr. Zeitels said that he had not received industry financial support for his research and that his team’s paper would be published in The Annals of Otology, Rhinology and Laryngology in July.

Original here

Sexy orchids do more than embarrass wasps?

Reuters Photo: A montage of orchids are on display at the 2005 Taiwan International Orchid Exhibition. Orchids...

WASHINGTON (Reuters) - Orchids that mimic female wasps may not only waste the time of the male wasps they lure into spreading their pollen -- they also seduce them into wasting valuable sperm, Australian researchers reported on Wednesday.

And the flowers benefit twice -- getting help in their own reproduction, and perhaps indirectly producing more male pollinators in the process.

Some of the most exotic orchids are known to have evolved their convoluted shapes to attract insects, who unwittingly collect and transfer pollen as they try to mate with the flowers.

"The effect of deception on pollinators has been considered negligible, but we show that pollinators may suffer considerable costs," Anne Gaskett of Macquarie University in Sydney and colleagues reported.

"Insects pollinating Australian tongue orchids (Cryptostylis species) frequently ejaculate and waste copious sperm," they wrote in a report in The American Naturalist.

It is not harmless to the wasps, who may suffer more than an inconvenience. "Male pollinators can prefer orchids to real females, prematurely end a copulation with a real female to visit an orchid, or be unable to find real female mates among false orchid signals," the researchers wrote.

"Unquestionably, producing sperm, ejaculate, or seminal fluids is costly for many animals. The energetic demands of sperm production can result in reduced body mass, a shortened life span, or limited lifetime sperm production," they added.

But this arms race of sexual trickery works in more than one way for the flower. "We also show that orchid species provoking such extreme pollinator behavior have the highest pollination success," they added.

"How can deception persist, given the costs to pollinators?"

They found that the wasps who frequent these flowers are haplodiploid species. Like bees, ants and similar species, offspring produced by sexual unions are female, while females can also produce males asexually.

"Therefore, female insects deprived of matings by orchid deception could still produce male offspring, which may even enhance orchid pollination," the researchers wrote.

Gaskett's team examined flowers after wasps visited them and found the hoodwinked males did eventually learn their lesson.

"With experience, male Lissopimpla excelsa wasps become less likely to copulate with and pollinate sexually deceptive Cryptostylis orchids," they wrote.

(Reporting by Maggie Fox; Editing by Eric Beech)

Original here

Plans for Large Hadron Collider visible in screen shot of first Web site

Remember the foreshadowing of the Death Star in Star Wars: Episode II? Check out this screen shot from the world's first Web site, http://info.cern.ch/, which went live 15 years ago on April 30, 1993.



Note the multicolored diagram in the background. That's an early schematic of ATLAS, one of two enormous particle detectors recently installed at the Large Hadron Collider (LHC), the 27-kilometer circular particle accelerator set to fire up later this year at CERN, the European Organization for Nuclear Research.



Web history buffs will recall that CERN was the place where physicist Tim Berners-Lee first dreamed up the World Wide Web, back in March 1989, hence the URL of the first Web site.

Seth Zenz, a University of California, Berkeley, grad student in physics who works on ATLAS, had read about the anniversary and was poking around the CERN site when he spotted the connection.

On the group blog US LHC, written by U.S. physicists working on the LHC, Zenz said the image was "an amazing reminder of just how long it takes to build a modern collider detector, and of just how different life was fifteen years ago." (He points out that you can now watch ATLAS via webcam.)

CERN continues to push computer networking to new heights. The Worldwide LHC Computing Grid is a global computer network—a shadow Internet, if you will—built to handle the 20-kilometer-tall-stack-of-CDs' worth of information the LHC will generate every year. Here's a cool interactive graphic that gives you the gist of the Grid. See also SciAm's 2003 feature on grid computing ($).

You can almost smell the future. If not the smoldering remains of Alderaan.
Original here