The Many Faces of Spin

Many of nature's deepest mysteries come in threes. Why does space have three spatial dimensions (ones that we can see, anyway)? Why are there three fundamental dimensions in physics (mass M, length L and time T)? Why three fundamental constants in nature (Newton's gravitational constant G, the speed of light c and Planck's constant h)? Why three generations of fundamental particles in the standard model (e.g. the up/down, charm/strange and top/bottom quarks)? Why do black holes have only three properties—mass, charge and spin? Nobody knows the answers to these questions, nor how or whether they may be connected. But some have sought for clues in the last-named of these properties: spin.

Spacetime is warped and twisted by the
mass and spin of the earth.

We are all familiar with rotation in the macroscopic world of tops, ballet dancers, planets and galaxies. Spin in the microscopic world is subtler, and obeys rules that are at once familiar (e.g. conservation of angular momentum) and bizarrely counter-intuitive (e.g. quantization and half-integer spin for fermions, which in the macroscopic world would correspond to objects that rotate through 720 rather than 360 degrees before returning to their original states). More abstract still are quantities like "isospin", which is analogous to ordinary spin in some ways but governs the behavior of the strong and weak nuclear forces (rotation through 180 degrees of isospin, for instance, converts a proton into a neutron), and torsion, a mathematical term related to the intrinsic twist of spacetime (this appears in some extensions of general relativity, but Einstein himself set it to zero in general relativity for reasons of logical economy). Are there connections between these manifestations of spin in the worlds of the large and small? Do they hint at the direction in which Einstein's theory of gravity might need to be extended in order to unify it with the other forces of nature? A generation of physicists since Einstein have thought about these questions, and they are part of the reason what makes Gravity Probe B so important, not just as another test of general relativity, but as a source of new insights about spacetime itself. Nobel laureate C.N. Yang wrote in a letter to NASA Administrator James M. Beggs in 1983 that general relativity, "though profoundly beautiful, is likely to be amended ... whatever [the] new geometrical symmetry will be, it is likely to entangle with spin and rotation, which are related to a deep geometrical concept called torsion ... The proposed Stanford experiment [Gravity Probe B] is especially interesting since it focuses on the spin. I would not be surprised at all if it gives a result in disagreement with Einstein's theory."

Back to Top

Gravito-Electromagnetism

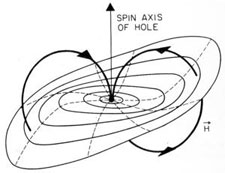
In general situations, space and time are so inextricably bound together in general relativity that they are hard to separate. In special cases, however, it becomes feasible to perform a "3+1 split" and decompose the metric of four-dimensional spacetime into a scalar time-time component, a vector time-space component and a tensor "space-space" component. When gravitational fields are weak and velocities are low compared to c, then this decomposition takes on a particularly compelling physical interpretation: if we call the scalar component a "gravito-electric potential" and the vector one a "gravito-magnetic potential", then these quantities are found to obey almost exactly the same laws as their counterparts in ordinary electromagnetism! (Although little-known nowadays, the idea of parallels between gravity and electromagnetism is not a new one, and goes back to Michael Faraday's experiments with "gravitational induction" beginning in 1849.) One can construct a "gravito-electric field" g and a "gravito-magnetic field H from the divergence and curl of the scalar and vector potentials, and these fields turn out to obey equations that are identical to Maxwell's equations and the Lorentz force law of ordinary electrodynamics (modulo a sign here and a factor of two there; these can be chalked up to the fact that gravity is associated with a spin-2 field rather than the spin-1 field of electromagnetism). The "field equations" of gravito-electromagnetism turn out to be of great value in interpreting the predictions of the full theory of general relativity for spinning test bodies in the field of a massive spinning body such as the earth — just as Maxwell's equations govern the behavior of electric dipoles in an external magnetic field. From symmetry considerations we can infer that the earth's gravito-electric field must be radial, and its gravito-magnetic one dipolar, as shown in the diagrams below:

These facts allow one to derive the main predictions of general relativity that are of relevance to Gravity Probe B, simply by replacing the electric and magnetic fields of ordinary electrodynamics by g and H respectively (for an illuminating discussion see Kip Thorne's contribution to Near Zero: New Frontiers of Physics, 1988). Based on this analogy the term "gravito-magnetic effect" is sometimes used interchangeably with "frame-dragging" (or with "Lense-Thirring effect"; see below). However any such identification must be treated with care because the distinction between gravito-magnetism and gravito-electricity is frame-dependent, just like its counterpart in Maxwell's theory. This means that observers using different coordinate systems (as, for example, one centered on the earth and another on the barycenter of the solar system) may disagree on the relative size of the effects they are discussing. Gravito-electromagnetism has already been indirectly observed in the solar system for some time, since general relativistic corrections are routinely used in, for instance, updating the ephemeris of planetary positions, and gravito-electromagnetic fields are nothing more than a necessary limit of Einstein's gravitational field in situations where gravity is weak and velocities are low. This is different from measuring a gravito-electromagnetic phenomenon like frame-dragging directly, which is one of the two primary goals of the Gravity Probe B mission.

Back to Top

Geodetic Effect

The geodetic effect provides us with a sixth test of general relativity (after the three classical tests plus Shapiro delay and the binary pulsar), and it is the first one to involve the spin of the test body. The effect arises in the way that angular momentum is transported through a gravitational field in Einstein's theory. Einstein's friend and colleague Willem de Sitter (1872-1934), who was instrumental in making general relativity known abroad, began to study this problem when the theory was less than a year old. He found that the earth-moon system would undergo a precession in the field of the sun, a special case now referred to as the de Sitter or "solar geodetic" effect (although "heliodetic" might be more descriptive). De Sitter's calculation was extended to rotating bodies such as the earth by two of his countrymen: in 1918 by the mathematician Jan Schouten (1883-1971) and in 1920 by the physicist and musician Adriaan Fokker (1887-1972).

De Sitter	Schouten	Fokker

In the framework of the gravito-electromagnetic analogy, the geodetic effect arises partly as a spin-orbit interaction between the spin of the test body (the gyroscope in the case of GP-B) and the "mass current" of the central body (the earth). This is the exact analog of Thomas precession in electromagnetism, where the electron experiences an induced magnetic field (in its rest frame) due to the apparent motion of the nucleus. In the gravitomagnetic case, the orbiting gyroscope feels the massive earth whizzing around it (in its rest frame) and experiences an induced gravitomagnetic torque, causing its spin vector to precess. This spin-orbit interaction accounts for one third of the total geodetic precession; the other two thirds arise due to space curvature alone and cannot be interpreted gravito-electromagnetically. They can, however, be understood geometrically. Model flat space as a 2-dimensional sheet, as shown in the diagram below (left).

Geodetic precession and the "missing inch"

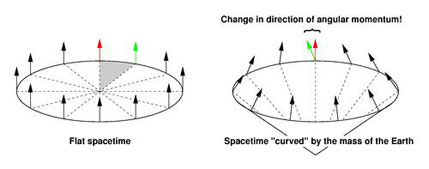
A gyroscope's spin vector (arrow) points at right angles to the plane of its motion, and its direction remains constant as the gyroscope completes a circular orbit. If, however, we fold space into a cone to simulate the effect of the presence of the massive earth (right), then we must remove part of the area of the circle (shaded) and the gyroscope's spin vector no longer lines up with itself after making a complete circuit (green and red arrows). The difference between these two directions (per orbit) makes up the other two thirds of the geodetic effect. In the case of Gravity Probe B this is sometimes referred to as the "missing inch" argument because space curvature shortens the circumference of the spacecraft's orbital path around the earth by 1.1 inches. In polar orbit at an altitude of 642 km the total geodetic effect (comprising both the spin-orbit and space curvature effects) causes a precession in the north-south direction of 6606 milliarcsec/yr — an angle so small that it is comparable to the average angular size of the planet Mercury as seen from earth.

Geodetic Effect

Experimental detection (or non-detection) of the geodetic effect will place new and independent limits on alternative theories of gravity known as "metric theories" (loosely speaking, theories that respect Einstein's equivalence principle). These theories are characterized by the Eddington or Parametrized Post-Newtonian (PPN) parameters β and γ, which are both equal to one in general relativity. The geodetic effect is proportional to (1+2γ)/3, so a confirmation of the Einstein prediction at the level of 0.01% would translate into comparable constraint on γ — more stringent than all but the most recent Shapiro time-delay test based on data from Cassini. Gravity Probe B observations of geodetic precession could also impose new constraints on other "generalizations of general relativity" such as the scalar-tensor theories pioneered by Carl Brans and Robert Dicke in 1961 (see Kamal Nandi et al, 2001). Another such class of theories incorporates torsion into Einstein's theory; examples have been proposed by Kenji Hayashi and Takeshi Shirafuji (1979), Leopold Halpern (1984) and Yi Mao et al. (2006). Another is based on extending the theory to higher dimensions; constraints on such theories arising from the geodetic effect have been discussed by Dimitri Kalligas et al. (1995) and Hongya Liu and James Overduin (2000). The most recent kind of generalization involves violations of Lorentz invariance, the conceptual foundation of special relativity; implications of such theories for Gravity Probe B have been worked out by Quentin Bailey and Alan Kostelecky (2006).

Back to Top

Frame-Dragging Effect

Lense

Thirring

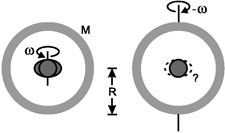
The frame-dragging effect, the seventh test of general relativity and the second one to involve the spin of the test body, reveals most clearly the Machian aspect of Einstein's theory. In fact, it is curious that Einstein did not work out this effect himself, given that he had obtained explicit frame-dragging effects in all his previous attempts at gravitational field theories, and that he still regarded Mach's principle as the philosophical pillar of general relativity in 1918. Whatever the reason, it was not until that year that the general-relativistic frame-dragging formula was derived by Hans Thirring (1888-1976) and Josef Lense (1890-1985), after whom the effect is now usually named. In an ironic twist, Thirring had not intended to do calculations at all; he had wanted to build a frame-dragging experiment (a cylindrical version of Föppl's flywheel experiment) and only settled for theoretical work after he was unable to arrange the necessary financing (see Herbert Pfister's contribution to Mach's Principle: From Newton's Bucket to Quantum Gravity, 1995). Thirring's initial result described the gravitational field inside a rotating cylinder; his second calculation (with Lense) involved the field outside a slowly rotating solid sphere and forms the basis for experimental tests such as Gravity Probe B. Both results are "Machian" in the sense that the inertial reference frame of a test particle is strongly influenced by the properties of the larger mass (the cylinder or sphere). This is completely unlike Newtonian dynamics, where a test particle's inertia is defined only by its motion with respect to "absolute space" and is unaffected by the distribution of matter. In fact, with the right parameters it is possible for a large mass in general relativity to completely "screen" the background geometry, so that a test particle feels only the reference frame defined by that mass. This phenomenon is known as "total" or "perfect dragging" of inertial frames (more on this below).

Frame-dragging Effect

Frame-dragging in realistic experimental situations is not nearly that strong and the utmost ingenuity has to be exercised to detect it at all. Analyzed in terms of the gravito-electromagnetic analogy, the effect arises due to the spin-spin interaction between the gyroscope and rotating central mass, and is perfectly analogous to the interaction of a magnetic dipole μ with a magnetic field B (the basis of nuclear Magnetic Resonance Imaging or MRI). Just as a torque μ×B acts in the magnetic case, so a gyroscope with spin s experiences a torque proportional to s×H in the gravitational case. For Gravity Probe B, in polar orbit 642 km above the earth, this torque causes the gyroscope spin axes to precess in the east-west direction by a mere 39 milliarcsec/yr — an angle so tiny that it is equivalent to the average angular width of the dwarf planet Pluto as seen from earth.

Back to Top

Genesis of GP-B

How small is 1/10th of a milliarcsecond?

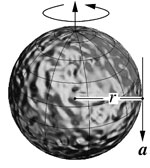
As the calculations of de Sitter, Schouten and Fokker became more widely known, particularly through Arthur Eddington's influential textbook The Mathematical Theory of Relativity (1923), experimentalists began to take interest. P.M.S. Blackett (1897-1974) considered looking for the de Sitter effect with a laboratory gyroscope in the 1930s, but concluded (rightly) that the task was hopeless with existing technology. To see what makes the problem so challenging, consider the gyroscope rotor shown below. The de Sitter effect and frame-dragging around the earth are both of order ~10 milliarcsec/yr, so to measure either of them with 1% accuracy requires that all unmodeled precessions on this rotor (known technically as the "drift rate") add up to less than 0.1 milliarcsec/yr, or 10^-18 rad/s. (See video clip "How smalll is 1/10th of a milliarcsecond?" at right.)

What does this requirement mean for our gyroscope? Precession Ω is related to torque τ by Ω=τ/(Iω) where I = (2/5)mr² is the moment of inertia and ω=v/r is the angular velocity. Inhomogeneities of size δr produce torques of order τ=maδr where a is the tangential acceleration. Combining these expressions gives a drift rate of Ω = (5/2)(a/v)(δr/r). Assuming a spin speed of v~1000 cm/s and accelerations comparable to those on the surface of the earth (a~g), the rotor must be homogeneous to within (δr/r) <>-17 to attain a drift rate less than 10^-18 rad/s! Such homogeneities are utterly unattainable on earth. In space, however, it is possible — just possible, with a great deal of work — to suppress unwanted accelerations on a test body by as much as eleven orders of magnitude, to a~10^-11g. If this can be done, then the gyro rotor need only be homogeneous to one part in 10⁶, rather than 10¹⁷ — a level that can be achieved, with great effort, using the best materials on earth.

Considerations of this kind led two people to take a new look at gyroscopic tests of general relativity shortly after the dawn of the space age. George E. Pugh (b. 1928) and Leonard I. Schiff (1915-1971) hit independently on the key ideas within months of each other. Pugh was stimulated by a talk given by Huseyin Yilmaz proposing a satellite test to distinguish his alternative theory of gravity from Einstein's, while Schiff was likely inspired at least in part by an advertisement for a new "Cryogenic Gyro ... with the possibility of exceptionally low drift rates" in Physics Today magazine (see Francis Everitt's contribution to Near Zero: New Frontiers of Physics, 1988). Pugh's paper, published in a Pentagon memorandum in November 1959, is now recognized as the birth of the concept of drag-free motion. This is a critical element of the Gravity Probe B mission, whereby any one of the gyroscopes can be isolated from the rest of the experiment and protected from all non-inertial forces; the rest of the spacecraft is then made to "chase after" the reference gyro by means of helium boiloff vented through a revolutionary porous plug and specially designed thrusters. In this way unmodeled accelerations on all the gyros, such as those resulting from the effects of solar radiation pressure and atmospheric friction on the spacecraft, can be reduced from a~10^-8g to below 10^-11g as required. (See animation clip "Drag-Free Motion" below.)

Schiff ~1970

Blackett	Pugh in 2007 Drag-free motion

The drag-free control system is only one of the innovations that made Gravity Probe B possible. The experiment depends on monitoring the precession of near-perfect gyroscopes relative to a fixed reference direction such as the line of sight to a distant guide star. But how is one to find the spin axis of a perfectly spherical, perfectly homogeneous gyroscope suspended in vacuum? This is the "readout problem"; another, closely related problem is how to spin up such a gyroscope in the first place. Various possibilities were considered in the early days, until 1962 when Francis Everitt and William Fairbank hit on the idea of exploiting what had until then been a small but annoying source of unwanted torque in magnetically levitated gyroscopes. Spinning superconductors develop a magnetic moment, known as the London moment, which is proportional to spin speed and always aligned with the spin axis. If the rotors were levitated electrically instead of magnetically, this tiny effect could be used to tell where their spin axes were pointed. (Measuring it would of course require magnetic shielding orders of magnitude beyond anything available in 1962, another story in itself.) Thus was born the London moment readout, which in its modern incarnation uses SQUIDs (Superconducting QUantum Interference Devices) as magnetometers. So sensitive are these devices that they register a change in spin-axis direction of 1 milliarcsec in five hours of integration time. (See animation clip "London Moment Readout" below.)

	">
London Moment readout	Dan Debra, Bill Fairbank, Francis Everitt and Bob Cannon with a model of Gravity Probe B, 1980

These are only two pieces of an experiment so beautifully intricate that it is as much a work of art as it is science and technology. Many of its key features reflect a guiding principle of physics experimenters through the ages, namely to turn obstacles into opportunities. How, for instance, can one meaningfully compare the gyroscope spin-axis direction (which is read out in volts) with the position of the guide star (which comes from an onboard telescope in radians)? The answer is to exploit nature's own calibration in the form of stellar aberration. This phenomenon, an apparent back-and-forth motion of the guide star position due to the orbit of the earth around the sun, is entirely Newtonian and inserts "wiggles" into the data whose period and amplitude are exquisitely well known (to give a sense of the precision of the experiment, the calibration requires terms of second, as well as first order in the earth's speed v/c). What about the fact that the guide star has an unknown "proper motion" large enough to obscure the predicted relativity signal? This allows the experiment to be designed in a classic "double-blind" fashion; a separate team of astronomers uses VLBI (Very Long-Baseline radio Interferometry) to monitor the movements of the guide star itself, relative to even more distant quasars. Only at the conclusion of the experiment are the two sets of data to be compared; this helps to prevent the physicists from "finding what they want to see."

For many more such examples, see the Unique Technology Challenges & Solutions page in the Technology tab. Gravity Probe B (or the Stanford Relativity Gyroscope Experiment, as it was known until 1971) received its first NASA funding in March 1964. The photograph above shows several of the early project leaders with a model of the spacecraft circa 1980: Dan Debra (a propulsion expert), Fairbank (the experimental low-temperature physicist par excellence), Everitt and Bob Cannon (a gyroscope specialist). See the History & Management section of the Mission page for more details.

Back to Top

Astrophysical Significance

Radio image of the giant jet
in NGC 6251

Artist's depiction of a
supermassive black hole

When Gravity Probe B was originally conceived, frame-dragging was seen as being of more theoretical than practical interest. To be sure, experimental confirmation of the Einstein (i.e. Lense-Thirring) prediction would place another independent constraint on alternative metric theories of gravity. Frame-dragging precession is proportional to the combination of PPN parameters (γ+1+α₁/4)/2 where γ describes the warping of space and α₁ is known as a "preferred-frame" parameter that allows for a possible dependence on motion relative to the rest frame of the universe (it takes the value zero in general relativity). However, frame-dragging is such a small effect in the solar system that experimental bounds it places on these parameters are not likely to be competitive with those from other tests. Confirmation of the Einstein (i.e. Lense-Thirring) prediction at the 1% level, for example, would translate into a comparable bound on γ and would not significantly constrain α₁.

Bardeen-Petterson effect

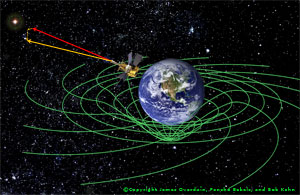
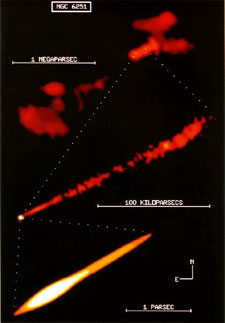
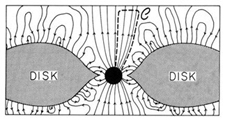
This situation has changed dramatically since the 1980s. Physicists now see frame-dragging as the gravitational analog of magnetism, and astrophysicists invoke this gravitomagnetic field as the engine and alignment mechanism for the vast and otherwise incomprehensible jets of gas and magnetic field ejected from quasars and galactic nuclei like the radio source NGC 6251, as shown above left. We know that these jets act as power sources for quasars and other strong extragalactic radio sources and that they are generated by compact, supermassive objects (almost certainly black holes) inside galactic nuclei, as illustrated above right. The megaparsec distance scale in the radio image above left implies that these compact objects are capable of holding the jet direction constant over timescale as long as ten million years. Black holes can only do this by means of their gyroscopic spin, and they can only communicate the direction of that spin to the jet via their gravitomagnetic field H. Such a field will cause an accretion disk to precess around the black hole, and that precession combined with the disk's viscosity should drive the inner region of the disk into the hole's equatorial plane, resulting in only two preferred directions for the jets: the north and south poles of the black hole. This phenomenon, known as the Bardeen-Petterson effect (diagram at left), is widely believed to be the physical mechanism responsible for jet alignment.

Blandford-Znajek effect

Kip Thorne discusses black holes
in the context of GP-B

Gravitomagnetism is also thought to explain the generation of the astounding energy contained in these jets in the first place. The event horizon of the black hole acts like a "gravitomagnetic battery", driving currents around closed loops like that shown in the diagram at left: up the magnetic field lines from the horizon to a region where the magnetic field is weak, across the field lines there, and then back down the field lines to the horizon and through the "battery" where the gravitomagnetic potential of the black hole interacts with the tangential component of the ordinary magnetic field B to produce a drop in electric potential (see Kip Thorne's contribution to Near Zero: New Frontiers of Physics, 1988). This phenomenon, known as the Blandford-Znajek mechanism, effectively draws on the immense gravitomagnetic, rotational energy of the supermassive black hole and converts it into an outgoing stream of ultra-relativistic charged particles. Gravity Probe B has thus become a crucial test of the mechanism that powers the most violent explosions in the universe.

Back to Top

Cosmological Significance

Star trails at night

Here is a simple experiment that almost anyone can perform on a clear night: pirouette freely around while looking up at the stars. You will notice two things: one, that the stars seem to spin around in the sky, and two, that your arms are pulled upwards by centrifugal force. Are these phenomena connected in some physical way? Not according to Newton. For him, centrifugal force is a consequence of accelerating (i.e. rotating) with respect to absolute space; it has no physical origin (and is therefore often called a "fictitious force" in elementary physics classes). It is, furthermore, a coincidence that the stars above us are at rest with respect to this same absolute space. We look upward, in effect, from two fundamentally different reference frames: one defined by our local sense of inertia, and the other defined by the global rest frame of the universe at large. Why should these two reference frames happen to coincide? Newton did not try to answer this question.

Kip Thorne discusses the significance
of GP-B for astrophysics & cosmology

We know that the concept of absolute space(time) is retained in general relativity, so we might have expected that the same coincidental alignment of our local inertial frame with that of the global matter distribution would carry over to Einstein's theory as well. Astonishingly, however, it does not. If general relativity is correct, then there are strong indications that our local "compass of inertia" has no choice but to be aligned with the rest of the universe — the two are linked by the frame-dragging effect. These indications do not come from experiment, but from theoretical calculations similar to that performed by Lense and Thirring. The calculations show that general-relativistic frame-dragging goes over to "perfect dragging" when the dimensions of the large mass (its size and density) become cosmological. In this limit, the distribution of matter in the universe appears sufficient to define the inertial reference frame of observers within it. For a particularly clear and simple explanation of how and why this happens, see The Unity of the Universe (1959) by Dennis Sciama. Had Mach lived 10 years longer, he could have predicted the existence of the extragalactic universe based on observations that the stars in the Milky Way rotate around a common center!

Would the earth still bulge, if it were
standing still and the universe were
rotating around it?

To put the cosmological significance of frame-dragging in concrete terms, imagine that the earth were standing still and that the rest of the universe were rotating around it: would its equator still bulge? Newton would have said "No". According to standard textbook physics the equatorial bulge is due to the rotation of the earth with respect to absolute space. On the basis of Lense and Thirring's results, however, Einstein would have had to answer "Yes"! In this respect general relativity is indeed more relativistic than its predecessors: it does not matter whether we choose to regard the earth as rotating and the heavens fixed, or the other way around: the two situations are now dynamically, as well as kinematically equivalent. The early calculations were flawed in many ways, but the phenomenon of perfect dragging has persisted in most subsequent, more sophisticated treatments, notably those of Helmut Hönl and Heinz Dehnen (1962, 1964), Dieter Brill and Jeffrey Cohen (1966) and Herbert Pfister and Karlheinz Braun (1986). Pfister sums up current thinking this way in Mach's Principle: From Newton's Bucket to Quantum Gravity (1995): "Although Einstein's theory of gravity does not, despite its name 'general relativity,' yet fulfil Mach's postulate of a description of nature with only relative concepts, it is quite successful in providing an intimate connection between inertial properties and matter, at least in a class of not too unrealistic models for our universe. Perhaps against majority expectation, this connection is instantaneous in nature. Furthermore, general relativity has brought us nearer to an understanding of the observational fact that the local inertial compass is fixed relative to the most distant cosmic objects, but there is surely desire for still deeper understanding." Thus does direct detection of frame-dragging by Gravity Probe B gain new importance: it will shine experimental light on what has heretofore been a theoretical mystery, namely the origin of inertia. For some, this is perhaps the most beautiful and profound manifestation of spin in Einstein's spacetime: it binds us here to the universe out there, in such a way that you, standing at night under the stars on a planet known as earth, cannot turn so much as around without feeling a tug from the rest of the universe.

Original here